Cálculo de recipientes a presión de pared delgada (página 2)

Cortemos una sección de longitud L

• De la figura se observa que las dF cos Ө se
  anulan
• También se observa que la dF sen Ө se suman,
  la suma de estas componentes verticales será

F=

  =pLr  

  =pLr

F=2pLr

O sea:

F =p L D

En ésta ecuación:

F= Fuerza
resultante debida a la presión
del fluido dentro del recipiente

p= Presión del fluido dentro del recipiente en
lb/pulg2

D= Diámetro del cilindro en pulgadas.

L= Longitud del recipiente

En esta ecuación se observa que LD es el área
proyectada en el plano horizontal de la media caña. Por lo
tanto la fuerza resultante es igual a la presión por el
área proyectada.

Ahora para encontrar P (fuerza en el aro)

,
pero F=pDL

Por lo tanto:

P=

P= prL

Para encontrar  (esfuerzo
de tensión en el aro)

=

En que:

Área = Área espesor de la pared en el aro
=tL

Y como P=p r L, tenemos

,
por lo tanto:

Cálculo del
esfuerzo longitudinal

• La fuerza de tracción T o fuerza longitudinal
  será

T= πr2p     
———————1)

En donde

T= Fuerza de tracción longitudinal

πr2= Área proyectada de la semiesfera
en un plano vertical

p= Presión del fluido dentro del recipiente

También:

T= ST22πrt 
………………..2), en que
2πrt = Área del espesor en la pared del anillo

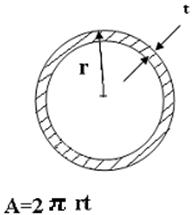
Igualando 1) con 2) tenemos:

ST2 2πrt=
π r2 p

ST2 2t =pr

Este es el esfuerzo longitudinal

Observamos que ST1= 2ST2

Por lo que para seleccionar el acero del
recipiente necesitaremos el mayor esfuerzo, o sea ST1

Caso tanques
esféricos

En este caso solo habrá ST2 que será con el que
se diseña.

MÁXIMO ESFUERZO CORTANTE
(SSmáx) EN LAS PAREDES DEL TANQUE SALCHICHA O
TUBO.

Usando el círculo de Mohr (no mostrado) encontramos

ST1= 2ST2= 2SSmáx

Ejemplo:

El cilindro mostrado en la figura, esta sujeto a una
presión interna de 400psi ( pounds per square inch) (lb
/pulg2). El diámetro del cilindro es de 30 pulgadas y el
espesor de la pared es media pulgada. ¿Cuál es el
esfuerzo de tensión más grande en el espesor de las
paredes?

RESPUESTA

El esfuerzo de tensión más grande será el
ST1 de acuerdo a lo que acabamos de ver

Datos:

P = 400psi

r = 15 pulg.

t = 0.5 pulg.

Incógnita

ST1= ¿

Ecuación:

ST1=

Sustituyendo valores
tenemos:

ST1=

ST1= 12 000 psi

Bibliografía

Fitzgerald, Robert W. Resistencia de materiales. Fondo Educativo Interamericano, S.
A. y Representaciones y Servicios de
Ingeniería, México,
1970

Sloane, Alvin. Mechanics of materials, The
MacMillanCo.EEUU,1960

Balanzá, Julio C. Resistencia de materiales teoría
y práctica. Universidad Veracruzana, Xalapa Ver.,
México, 1993.

Resumen

Se deducen las ecuaciones
para calcular los esfuerzos en las paredes de los cilindros de
pared delgada, tales como: los domos de las calderas, las
tuberías, los separadores de fluidos en la industria
petrolera, los tanques llamados "salchichas"y los tanque
esféricos llamados "esferas" en la industria petrolera. La
utilidad de
estos conocimientos está en el diseño
de los dispositivos mecánicos señalados, y en la
impartición de las materias de la carrera Ingeniero
Mecánico Electricista: Diseño Mecánico,
Resistencia de
materiales, Instalaciones mecánicas y otras afines. Se
resuelve un problema utilizando estos conocimientos

Datos del autor:

Nacimiento: 16 de mayo de 1941, Tampico, Tamaulipas,
México.

Jubilado del departamento de Mantenimiento
Equipo Dinámico e Instrumentos de PEMEX Exploración
Producción de Poza Rica, Veracruz, 
México.

Catedrático en el Instituto Tecnológico Superior
de Poza Rica y En la Facultad de Ingeniería Mecánica Eléctrica de la Universidad
Veracruzana en Poza Rica, Veracruz.

Títulos Obtenidos:

Ingeniero Mecánico Electricista de la Facultad Nacional
de Ingeniería de la UNAM

M en C. Diseño Mecánico, Mención
Honorífica en el IPN.

Certificante in "Professional Studies In Education" Issued By
Association Of Colleges, the Bradford College and the
Warwickshire college of the U.K.

Certificante in "English as a Foreign Languaje" Warwickshire
College, U.K.

Libros:

Diseño del Nuevo Alumbrado del parque de Base-Ball en
Poza Rica, Veracruz (Tesis
Licenciatura UNAM)

"Resistencia de Materiales Teoría y Problemas"
Editado por la Universidad Veracruzana.

"Diseño del Balancín Elevador de una Unidad de
Bombeo Mecánico Petrolera Mark II" (Tesis Maestría
en el IPN)

Autor:

M en C. Julio Cesar de Jesús Balanzá
Chavarria